Longueurs et périmètres.
Sommaire :
La longueur du segment [AB] se note :
AB = 5 cm.
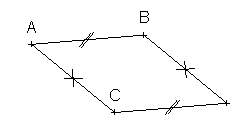
Si sur une même figure, plusieurs segments ont la même longueur, un utilise un symbole (/ ;// ;/// ;x ;o) placer au milieu du segment pour symboliser ces égalités de longuueurs :
Exemple :
Remarque : Pour reporter une longueur sans la mesurer, on utilise le compas.
Exercices 1,2,3, 28, 29 p 131
Définition :
Le périmètre d’une figure est la longueur de son contour.
Exemple :

Le périmètre de cette figure est la somme des longueurs des segments :
P = AB + BC + CD +
DE + EA
On peut calculer la longueur du
périmètre de certaines figures, mais il existe des figures où l’on trouve
seulement une valeur approchée de leur périmètre.

Figure
de très grand périmètre inscrite dans un carré (Koch)
8 et 9 p 131
Lorsque l’on calcule des
périmètres, on additionne des longueurs. Les unités utilisés sont donc des
unités de longueurs : mètre (m) ;
décamètre (dam), hectomètre (hm)…
Pour effectuer des changements
d’unités, on utilise un tableau :
|
km |
hm |
dam |
m |
dm |
cm |
mm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Placer dans le tableau les longueurs
suivantes :
1,024 km ; 3,5 dam ;
0,025 hm ; 1 250 000 mm.
Compléter à l’aide du
tableau :
25 m = …… hm 0,15
km = …… dm
0,0015 hm = ……m 2,03
m = …… mm
Remarque: On peut également
utiliser les multiplications et divisions par 10, 100, 1000 pour faire les
conversions.
Dm avec pouce, lieu... (banqoutil)
4,5,6 p 131
30,31,32 (oralement)
a.
Les quadrilatères
Le rectangle: P
= 2L + 2l = 2 (L + l)
Le losange ou le carré : P = 4c
23, 35 p 133
b.
Le cercle
Activité :
Ramener des cercle (couvercle, bouteille...) et un mètre de couture.
La longueur
d’un cercle est donnée par la formule :
P = 2×π×r =
π×d où π ≈ 3,1415
13, 14, 15, 34, 36, 38, 39 p 135
53 p 136 en DM ;55 p 136