Chapitre 2 : Opérations sur les
fractions
Sommaire :
1.
Additions et soustractions de fractions
Règle d’addition et de
soustraction :
Pour additionner ou soustraire deux
fractions, il faut les mettre au même dénominateur puis additionner (ou
soustraire) les numérateurs. Ensuite, on simplifie le résultat (si c’est
possible).
Exemple : calculer
![]()
19, 20, 29 p 56.
1.
Multiplication de fractions
On considère un carré de 1 mètre de coté (faire tracer un carré de côté 5 cm).
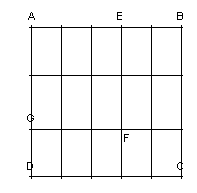
· Quelle est l‘aire du carré ABCD ?
· Placer le point E situé au 3/5 de [AB]et placer le point G situé au 2/3 de [AD].Compléter la figure pour obtenir un rectangle AEFG.
· Quelle fraction de l’aire du carré représente chacun des petits rectangles du quadrillage ?
· Quelle est l’aire du rectangle AEFG ?
· En utilisant la formule : Aire (rectangle) = L × l, exprimer l’aire du rectangle sous la forme d’un produit de fractions.
En déduire que
![]()
Règle de multiplication :
Pour multiplier deux fractions, on multiplie
les numérateurs et les dénominateurs entre eux. (puis on simplifie si
possible).
8, 9 p 55
Exemple :
![]()
Observer les deux derniers calculs.
Remarque : Dans la pratique, on préfère regarde s’il existe des simplifications avant de multiplier :
![]()
10, 12, 14 p 55
31,32,33 p 56
47 en DM
Exemple 1 :
Dans une classe de 24 élèves, il y a 8 élèves qui ont entre 10 et 15 et 4 élèves entre 15 et 20.
Combien d’élèves ont plus de 10 ?
Réécrire l’énoncé en utilisant des fractions.
Exemple 2 :
Dans une classe de 21 élèves, deux tiers n’ont pas doublé. Combien sont-ils ?
Exemple 3 :
Dans une classe de 24 élèves, 16 élèves ont la moyenne dont un quart a plus de 16.
Combien d’élèves ont plus de 16 ?
Réécrire l’énoncé à l’aide de fractions.
36,37,38,39 p 56
58, 60, 63 p 58